logistic regression

前面的课程学习了线性回归，可以用于预测房价这一类的问题。预测房价这种问题是连续的而且值域是[0,+∞]。但是生活中并不仅是有这类问题，还有一类非常常见的问题种类叫做分类问题。比如说对常见的对邮件进行分类是正常邮件还是垃圾邮件等等。在这节课程中学习使用logistic regression来处理这种问题。

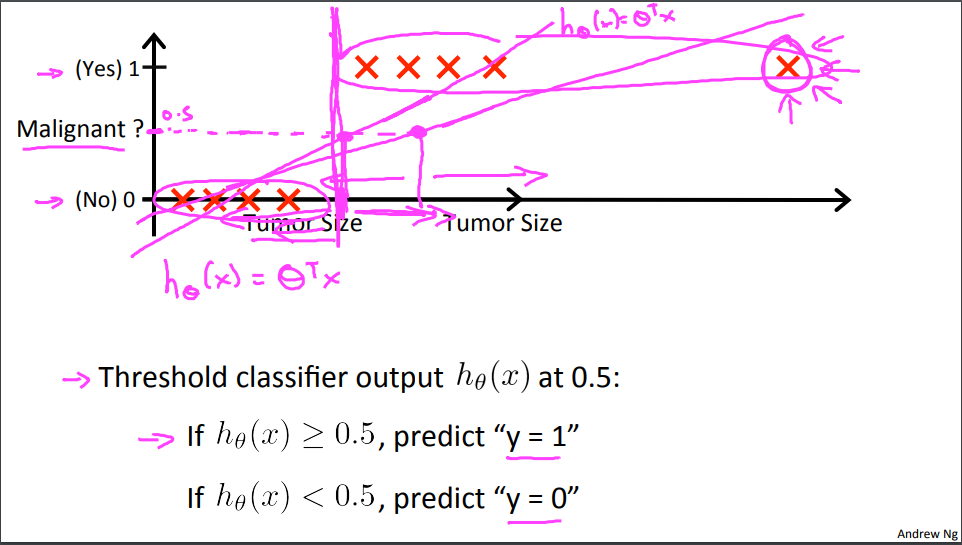
首先在学习logistic regression之前课程通过一个简单的例子来告诉我们为什么线性回归不适合分类问题。

在这个例子中将正类的值设为1，负类的值设为0，使用中间值0.5作为判断界限。我们可以看到使用线性回归对异常值非常的敏感，在在第二次线性回归的时候因为异常值出现，导致最终判断的界限出现了较大的偏差，分类出现问题。因为线性回归其输出值域是[-∞,+∞],二一个二分类问题其值域为{0，1}.直接使用线性回归的方法去训练就会出现较大的问题。解决的方法是找到一个函数将线性回归输出的z映射到{0，1}。其中最理想的函数的单位单位阶跃函数，表达如下：

$f(x)= \begin{cases} 0,&z<0\\ 0.5,&z=0\\ 1,&z>0 \end{cases} \tag{1}$

这样就将线性回归的输出值映射到了{0，1}，但是这个函数不是连续的这样在后面训练的时候就非常不好处理。然后前辈先人们希望找到一个和它非常相似的一个函数，同时数学性质要比较好要单调可微，然后他们就找到了非常著名的Sigmoid函数，就和它的首字母一样函数的形状就像一个横过来S的Sigmoid函数

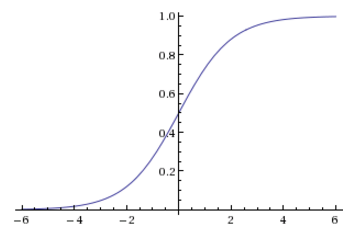
这样logistic regression的假设函数就确定了是

$h_θ(x)=g(θ^Tx) \tag{2}$

其中$g(x)$也就是前面提到的sigmoid函数，中间的$θ^Tx$也就是原来的线性回归部分。

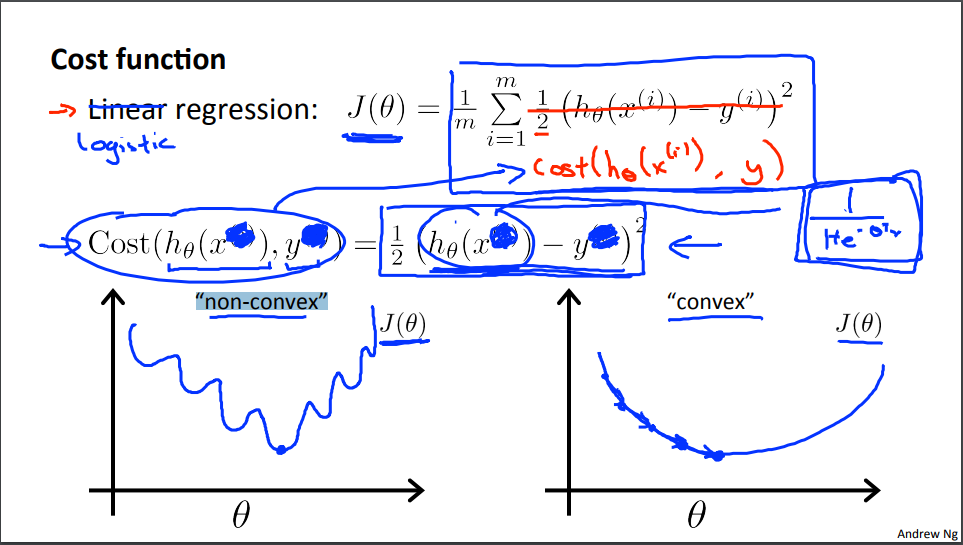
然后在课程中提到了一个东西叫做Decision Boundary（决策边界），当函数中的θ确定也就确定了一个边界，边界将数据划分成了两类。这个边界在一维中就是一个点，二维就是一条线… 我们要做的就是从训练数据找到一个合适的边界，来将数据分类。具体来说当你确定你想要的$h_θ(x)$,之后就是需要去寻找一个合适的θ。下面需要要确定一个cost function，来对选择的θ进行评估。原来线性回归用的是最小二乘法，在逻辑回归中用的是极大似然的方法。课程老师解释不用最小二乘法的原因的因为使用最小二乘法的cost function是非凸的在求最优解的时候很容易进入到局部最小，而最大似然则没有这个缺点。具体的原因我也还是不是很清楚，等知识充足了理解了再来更新，现在就先用着吧。

使用最大似然的方法计算代价函数的公式如下所示：

$Cost(h_\theta(x),y)= \begin{cases} -log(h_\theta(x)) &if\quad y=1\\ -log(1-h_\theta(x)) &if\quad y=0 \end{cases}\tag{3}$

我们可以看到$Cost(h_\theta(x),y)$无论对于y是0还是1，都是当$h_\theta(x)$接近时趋近与0而但远离时趋近与+∞。
整合合并后最终的cost function的的公式如下：

$J(θ)=\frac{-1}{m}[\sum_{i=1}^my^{(i)}logh_θ(x^{(i)})+(1-y^{(i)}）log(1-h_θ(x^{(i)}))] \tag{4}$

---

2018年8月2日更新

最大似然法是概率论中进行参数估计的一种方法。它的使用方式可以用一句话来概括：寻找使得样本观测值出现概率最大的参数θ。这里有一个默认的假设就是认为抽样得到的样本观测者是所有可能的样本观测值中出现概率最大的那组。
在logistic regression中$h_θ(x)$标识y=1的概率，因而总体Y的分布律为：

$P(Y=K)=h_θ(x)^k(1-h_θ(x))^k,\qquad k=0,1 \tag{5}$

最终得到其似然函数为：

$L(θ)=\prod_{i=1}^nP(Y_i=y_i,θ) \tag{6}$

对公式$(6)$取对数就可以得到公式$(4)$方括号中的部分了，因为梯度下降时一般是求min所以带上了负号。

---

知道这个之后我们就可以使用梯度下降的方法来求解最合适的θ值了。方法和前面的线性回归是一样的。其中cost function对θ的偏导如下所示：

$\frac{\partial }{\partial \theta_j}J(\theta) =\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \tag{7}$

求得θ之后什么也就得到了确定的$h_\theta(x)$我们可以将需要分类的数据带入其中就可以得到这个数据点近似预测概率，在二分类中一般取大于等于0.5预测为正，小于则为负。

在使用logistic regression做多分类问题时，每次只看一类作为正的其他的统统视为负的，最有n个类别就得到n个logistic回归函数。在预测时选择选择概率最高的那个作为预测结果，在这里我们也看看出输出结果为预测概率的好处，如果只是单纯判别是或者不是那么在使用二分类组合成多分类时就很可能出现无法判断的情况。